هياكل البيانات الشجرية Trees Data Structure

هياكل البيانات الشجرية Tree Data Structure

من بين أهم وأقوى الخوارزميات في علم الحاسب تأتي الأشجار (Trees) متمثلة في هياكل البيانات الشجرية (Trees Data Structure)، حيث أن الأشجار Trees دورًا محوريًا في تنظيم البيانات بشكل يساعد على تحسين الكفاءة وسرعة الوصول إلى المعلومات…. فما هو مفهوم الأشجار في الخوارزميات … ؟؟!! كيف نعرفها وما أهم أنواع هياكل البيانات الشجرية Trees Data Structure…!! ومع أي التطبيقات يمكن أن نستخدم هياكل البيانات الشجرية (Trees Data Structure)..!!!

في مفاهيم علوم الحاسب أو الخوارزميات تحديداً تمثل الشجرة (Tree) نوع من أنواع هياكل البيانات فهي بنية بيانات غير خطية تتكون من العقد (Nodes) والوصلات (Edges) التي تربط بينها، بحيث تتيح ترتيب البيانات في هيكل هرمي أو شبكي. تستخدم هذه البنية في مجالات متعددة، مثل إدارة قواعد البيانات، تمثيل العلاقات الهرمية في النظم، تطبيقات الذكاء الاصطناعي، والخوارزميات المتقدمة. يقدم هذا المقال نظرة على هياكل البيانات الشجرية (Trees Data Structure). لنبدأ…

في هذا المقال نتعرف على :

• هياكل البيانات الشجرية (Trees Data Structure).
• مصطلحات في هياكل البيانات الشجرية Tree Terminology.
• أنواع الأشجار في هياكل البيانات الشجرية (Trees Data Structure).
• تطبيقات هياكل البيانات الشجرية (Trees Data Structure).
• تنفيذ الشجرة Tree Implementation.

هياكل البيانات الشجرية Trees Data Structure

إن هياكل البيانات الشجرية (Tree Data Structure) أو بنية بيانات الشجرية هي بنية هرمية الشكل تُستخدم لتمثيل البيانات وتنظيمها بطريقة يسهل التنقل عبرها والبحث فيها. ويمكن أن تُعرف هياكل البيانات الشجرية على أنها نوع من أنواع هياكل البيانات (المزيد عن هياكل البيانات في مقال  مقدمة الى هياكل البيانات) الغير خطية يتم فيها ربط مجموعة من العناصر المعروفة باسم العقد Nodes بالتي تتصل بعضها البعض عبر حواف (Edges) بحيث يوجد مسار واحد بالضبط بين أي عقدتين.

يمكن أن تشبه بنية بيانات الشجرية (Tree Data Structure) القوائم المرتبطة Linked list حيث تحتوي كل عقدة على بيانات ويمكن ربطها بالعقد الأخرى. في الشجرة،و يمكن أن يحتوي العنصر الواحد على عناصر "تالية" متعددة، مما يسمح لبنية البيانات بالتفرع في اتجاهات مختلفة.لهذا تسمى بنية البيانات "بالشجرة Tree" لأنها تبدو مثل شجرة، فقط مقلوبة رأسًا على عقب.تماماً كما هو موضح في المثال الظاهر بالشكل التالي:

أي أن هياكل البيانات الشجرية Tree Data Structureعبارة عن مجموعة من العقد Nodes المرتبطة ولها علاقة هرمية بين العقد. حيث تسمى العقدة العليا في الشجرة بالجذر (Root) ، وتسمى العقد الموجودة أسفلها بالعقد الفرعية. ويمكن أن تحتوي كل عقدة على عقد فرعية متعددة، ويمكن أن تحتوي هذه العقد الفرعية أيضًا على عقد فرعية خاصة بها، مما يشكل بنية متكررة.

وتعتبر هياكل البيانات الشجرية من أبرز وأهم هياكل البيانات في علوم الحاسوب، وهذا للطريقة التي تعمل بها في تنظيم البيانات حيث تمكن من الوصول السريع والفعال إليها.كما يتم استخدام الأشجار(Trees) في العديد من التطبيقات التي تتطلب هيكلة البيانات بشكل هرمي، مثل قواعد البيانات، نظم الملفات، وبعض الخوارزميات المتقدمة. والهدف الأساسي من استخدام الأشجار هو تحسين كفاءة عمليات البحث، الإدراج، والحذف، مقارنةً ببعض الهياكل الأخرى.

مصطلحات في هياكل البيانات الشجرية (Tree Terminology)

يوجب العمل مع هياكل البيانات الشجرية Tree data structure على فهم بعض المفاهيم والمصطلحات مثل أسماء العُقد (Nodes)، حيث تأخذ العُقد Nodes أسماء بحسب ترتيب مواقعها في الشجرة (Tree) ، ويوضح الشكل التالي مسميات العُقد في الشجرة :

• العقدة الأصل ( Parent Node): العقدة السابقة للعقدة تسمى العقدة الأصل لتلك العقدة، وتسمى أيضاً عقدة الأب أو الأم ، مثلاً العقدة {B} هي العقدة الأصل لـ {E, F}.
• العقدة الفرعية (Child Node): تسمى العقدة التي ترتبط بعقده معينة وتأتي في المستوى التالي لتلك للعقدة بالعقدة الفرعية لتلك العقدة وتعرف باسم عقدة الابن، مثلاً : العقدتين {E, F} هي عُقد فرعية لـ {B}.
• عقدة الجذر(Root Node): تسمى العقدة العليا للشجرة أو العقدة التي لا تحتوي على أي عقدة أصل بعقدة الجذرroot، والعقدة {A} هي العقدة الجذر للشجرة في المثال .ويجب أن تحتوي الشجرة غير الفارغة على عقدة جذر واحدة بالضبط ومسار واحد بالضبط من الجذر إلى جميع العقد الأخرى في الشجرة.
• العقدة الطرفية أو الخارجية (Leaf Node or External Node): تسمى العقد التي لا تحتوي على أي عقد فرعية بالعقد الطرفية أو الخارجية وتعرف بالأوراق فهي عُقد نهائية و تتمثل في المثال بـ {E, F، G، H، I، K} هي العقد الورقية للشجرة.
• عُقدة السلف (Ancestor of a Node): أي عقد سابقة على مسار الجذر إلى تلك العقدة تسمى أسلاف تلك العقدة ففي المثال تعتبر {A,D, J} هي أسلاف للعقدة {K}
• الابناء والاحفاد (Descendant): جميع العقد الفرعية والعقد المتفرعة منها. في المثال Descendant(D)= {J,K}
• الأخوة (Sibling): العُقد التي تتشارك من نفس العقدة الأصل يطلق عليهم الأشقاء ، مثلاً {G, H, I} يطلق عليهم الأشقاء.
• العقدة الداخلية (Internal node): تسمى العقدة التي تحتوي على فرع واحد على الأقل بالعقدة الداخلية، ففي المثال تعتبر العقد B, C, D, J عُقد داخلية
• العقدة المجاورة (Neighbor of a Node):العُقد المتصلة بعقدة معينه مثل عقد الأصل أو العقدة الفرعية لتلك العقدة تعتبر جيران لتلك العقدة، على سبيل المثال تعتبر D و J جيران بينم

أيضاً هنالك العديد من المصطلحات الخاصة بهياكل البيانات الشجرية Tree data structure ومنها ما يتضح في الشكل التالي:

• الحواف (Edges) : في هياكل البيانات الشجرية يُعبرعن المواصلات بين العُقد بمصطلح حافة أو الحواف (An edge or edges).
• مستوى العقدة (Level of a node): عدد حواف (Edges) المسار من العقدة الجذرية إلى تلك العقدة، العقدة الجذرية لديها المستوى 0.
• الشجرة الفرعية ( Subtree): أي عقدة من الشجرة مع تفرعاتها.
• درجة العقدة (Node Degree ): درجة العقدة هي عدد الأبناء (ChildNodes) لديها.
• ارتفاع العقدة (Node Height) : في هياكل البيانات الشجرية، يُعرف عدد الحواف (edges) من العقدة الطرفية إلى عقدة محددة في بإرتفاع تلك العقدة.
• عمق العقدة (Node Depth): في هياكل البيانات الشجرية، يُعرف عدد الحواف (edges) من العقدة الجذرية root إلى عقدة محددة بعمق تلك العقدة.

من خصائص هياكل البيانات الشجرية Tree Data Structure التالي:

• في هياكل البيانات الشجرية يمكن حساب عدد الحواف (Number of edges )، فإذا كانت الشجرة تحتوي على عدد N من العُقد ، فسيكون لها عدد الحواف edges لها يساوي (N-1)، أي يوجد مسار واحد فقط من كل عقدة إلى أي عقدة أخرى في الشجرة.
• بما انه في هياكل البيانات الشجرية ، يتم تعريف الـ Node Depth أيضًا على أنه عدد الحواف (edges) في المسار من جذر الشجرة إلى العقدة، فعند إضافة عقدة جديدة تضاف حافة (edge) واحدة إلى طول المسار. لذلك، يمكن تعريف عمق العقدة (Node Depth) على أنه طول المسار من الجذر إلى تلك العقدة.
• في هياكل البيانات الشجرية، يُعرف المسار الأطول لإجمالي عدد الحواف Edges من العقدة الجذرية (root) إلى عقدة طرفية باسم عمق الشجرة (Depth of the Tree).
• في هياكل البيانات الشجرية دائماً يكون العمق العقدة الجذرية (Root node depth ) يساوي 0.
• في هياكل البيانات الشجرية يمكن تعريف ارتفاع العقدة (Node Height)على أنه طول المسار من العقدة إلى العقدة الورقية للشجرة.
• في هياكل البيانات الشجرية يُسمى ارتفاع العقدة الجذرية "ارتفاع الشجرة" (Height of the Tree).
• في هياكل البيانات الشجرية، إن ارتفاع العقدة لجميع العقد الورقية (leaf nodes) هو 0.
• في هياكل البيانات الشجرية، يُطلق على إجمالي عدد الأشجار الفرعية المرتبطة بتلك العقدة درجة العقدة (Degree of a Node).
• درجة الشجرة (Tree Degree) هي أقصى درجة عقدة بين جميع العقد في الشجرة.
• في هياكل البيانات الشجرية Tree data structure يجب أن تكون درجة العقدة الورقية 0.

إن فهم مصطلحات هياكل البيانات الشجرية (Tree Terminology) يعد أمرًا مهم لأي مطور أو مهندس برمجيات يسعى للتعامل بفعالية مع هذه الهياكل. فمن خلال معرفة المفاهيم الأساسية مثل العقد (Nodes)، الجذور (Roots)، الأوراق (Leaves)، والعقد الداخلية (Internal Nodes)، باختصار، الإلمام بمصطلحات هياكل البيانات الشجرية يفتح الباب أمام استغلال إمكانياتها الواسعة في تحسين أداء التطبيقات البرمجية وتطوير حلول ذكية وفعالة.

أنواع هياكل البيانات الشجرية

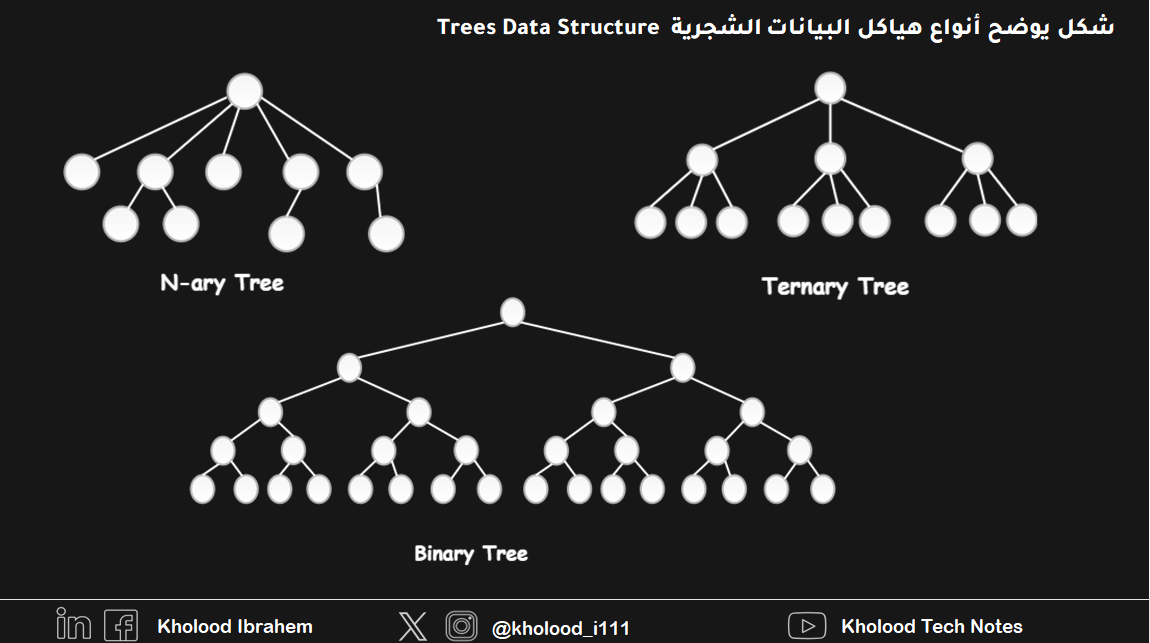
لهياكل البيانات الشجرية أو بنية البيانات الشجرية (Tree Data Structure) عدة أشكال لكل منها مميزاته يوضح الشكل التالي أهم ثلاثة أنواع مصنفة بناءً على عدد الأبناء الذين يمكن أن تنالهم كل عقدة من الشجرة:

الشجرة العامة أو شجرة  Generic Tree or N-ary Tree:

الأشجار العامة (General trees) هي هياكل بيانات شجرة غير مرتبة حيث تحتوي العقدة الجذرية على الحد الأدنى من 0 أو الحد الأقصى من الأشجار الفرعية 'N'. والأشجار العامة لا يمكن أن تكون فارغة و ليس لها أي قيود على تسلسلها الهرمي. وبالتالي فإن العقدة الجذرية تعمل مثل المجموعة الشاملة لجميع الأشجار الفرعية الأخرى.

وتُعرف الشجرة العامة بشجرة N-ary فهي مجموعة من العقد حيث تكون كل عقدة عبارة عن بنية بيانات تتكون من سجلات وقائمة مراجع لأطفالها (غير مسموح بالمراجع المكررة). على عكس القائمة المرتبطة، تقوم كل عقدة بتخزين عنوان العقد المتعددة.

الشجرة الثنائية Binary Tree:

الأشجار الثنائية أشهر نوع من أنواع بنية بيانات الشجرية Trees data Structure ، وسميت بالشجرة الثنائية (binary tree) لأن كل عقدة تحتوي على عقدتين فرعيتين كحد أقصى، عقدة فرعية يسرى وعقدة فرعية يمنى. أي لا يجوز لأي عقدة في الشجرة الثنائية أن تحتوي على درجة أكثر من 2 بينما لا يوجد حد لدرجة العقدة في الشجرة.

وقد تكون الأشجار الثنائية فارغة (عُقد بدون قيم)، ويجب أن تكون الأشجار الفرعية للشجرة الثنائية مرتبة، وتعتبر الأشجار الثنائية (Binary Trees) أهم أنواع هياكل البيانات الشجرية (Trees data Structure) فهي تتضمن أنواع عدة من هياكل البيانات الشجرية، ويمكن تصنيف الشجرة الثنائية إلى أنواع متعددة بناءً على عوامل متعددة، مثلاً :

يكون تصنيف أنواع الأشجار الثنائية Binary Tree على أساس المستويات (Levels)، كتالي:

• أشجار ثنائية كاملة (Complete Binary Trees).
• أشجار ثنائية مثالية ( Perfect Binary Trees).
• أشجار ثنائية متوازنة ( Balanced Binary Trees)

بينما يكون تصنيف أنواع الأشجار الثنائية Binary Tree على أساس عدد الأطفال (Child Nodes) ، كتالي:

• أشجار ثنائية ممتلئة (Full Binary Trees).
• أشجار ثنائية متدهورة أو مرضية (Degenerate Binary Trees).
• الأشجار الثنائية المنحرفة (Skewed Binary Trees).

بينما يكون تصنيف أنواع الأشجار الثنائية Binary Tree على أساس قيم العقدة (Node):

• شجرة البحث الثنائية (Binary Search Tree).
• شجرة AVL ( AVL Tree).
• شجرة حمراء سوداء (Red Black Tree).
• شجرة الشرائح ( Segment Tree).

الشجرة الثلاثية (Ternary Tree):

الشجرة الثلاثية Ternary Tree هي بنية بيانات الشجرية التي تحتوي كل عقدة فيها على ثلاث عقد فرعية على الأكثر، وعادة ما يتم تمييزها على أنها "يسار" و"منتصف" و"يمين" (left, mid and right).

إن هياكل البيانات الشجرية (Tree Data Structures) من هياكل البيانات الأساسية في علم الحاسب، ويظهر هذا تتنوع أنواع الأشجار حيث أن كل نوع منها يخدم أغراضًا محددة ويقدم مزايا خاصة، مما يجعلها مناسبة لمجموعة واسعة من التطبيقات بدءًا من أنظمة الملفات وقواعد البيانات، وصولاً إلى الذكاء الاصطناعي وتحليل البيانات. ففهم هذه الهياكل واستخدامها بشكل صحيح يسهم بشكل كبير في تحسين أداء النظم والتطبيقات الحاسوبية.

تطبيقات هياكل البيانات الشجرية

لهياكل البيانات الشجرية (Trees data Structure) العديد من التطبيقات في مجالات متنوعة. فيما يلي بعض التطبيقات البارزة:

• أنظمة الملفات File Systems: تُستخدم هياكل البيانات الشجرية لتنظيم الملفات والمجلدات في أنظمة التشغيل. الشجرة هنا تمثل التسلسل الهرمي للمجلدات والملفات، مما يتيح التنقل الفعال وتنظيم الملفات. (المزيد عن أنظمة الملفات في مقال عن سطر أوامر لينكس)
• تحليل الشفرات Parsing: في المترجمات (Compilers) والمفسرات (Interpreters)، تُستخدم هياكل البيانات الشجرية لتحليل الشفرات المصدرية (ٍsource code) إلى ما يمثلها داخلياً ، مثل شجرة التحليل النحوي (Parse Tree) أو شجرة بناء الجمل المجردة (Abstract Syntax Tree - AST). أي في تصميم المترجم، يتم استخدام شجرة بناء الجملة لتمثيل بنية البرنامج.
• محركات البحث Search Engines: تُستخدم هياكل البيانات الشجرية المقطعية (Tries) في محركات البحث لتسريع عمليات البحث عن الكلمات والكلمات المشتقة.
• الذكاء الاصطناعي Artificial Intelligence : أهم خوارزميات الذكاء الاصطناعي تعتمد هياكل البيانات الشجرية، فتُستخدم أشجار اتخاذ القرار (Decision Trees) لتمثيل القرارات الممكنة وتبعاتها في الألعاب والذكاء الاصطناعي.
• الشبكات Networks : مع بناء الشبكات تُستخدم هياكل البيانات الشجرية (Trees data structure) في بروتوكولات التوجيه (Routing Protocols) لتنظيم وتوجيه حزم البيانات بين الشبكات.
• الرسوميات الحاسوبية Computer Graphics :تُستخدم هياكل البيانات الشجرية في تقسيم المشاهد الرسومية إلى أجزاء أصغر، مثل شجرة Octree في الرسوميات ثلاثية الأبعاد، لتسريع عمليات التصيير (Rendering).
• قواعد البيانات Databases: تُستخدم هياكل البيانات الشجرية، مثل B-trees وB+ trees، في تنظيم البيانات والفهارس لتسهيل وتسريع عمليات الاستعلام.( المزيد عن قواعد في مقال مقدمة إلى قواعد البيانات).
• إدارة الذاكرة Memory Management: تُستخدم الأشجار الثنائية المتوازنة ( Balanced Binary Trees)، مثل AVL trees، في تخصيص وإدارة الذاكرة الديناميكية بكفاءة.
• تحليل البيانات Data Analysis: تُستخدم الأشجار في تحليل البيانات واستخراج الأنماط، مثل شجرة القرار (Decision Trees) في التنقيب عن البيانات (Data Mining).
• هياكل البيانات الديناميكية : تُستخدم الأشجار مثل الأشجار المقطعية (Suffix Trees) والأشجار المتوازنة في تنظيم النصوص وتحليلها بكفاءة، مما يسهم في تحسين أداء التطبيقات التي تتعامل مع النصوص بشكل مكثف.
• التطبيقات الجغرافية Geographical Applications :تُستخدم الأشجار مثل R-trees في نظم المعلومات الجغرافية (GIS) لتنظيم البيانات الجغرافية وتحسين عمليات البحث المكاني.
• البريد الإلكتروني Email Systems : تُستخدم الأشجار لتنظيم الرسائل البريدية في مجلدات، وإدارة قواعد البيانات البريدية بكفاءة.
• ضغط البيانات Data compression: يعد ترميز هوفمان أسلوبًا شائعًا لضغط البيانات يتضمن إنشاء شجرة ثنائية حيث تمثل الأوراق والحواف وتكرار حدوثها. يتم استخدام الشجرة الناتجة لترميز البيانات بطريقة تقلل من حجم التخزين المطلوب.

إن استخدام هياكل البيانات الشجرية مع التطبيقات البرمجية يساعد في تحسين أدائها فمن خلال تنظيم البيانات بشكل هرمي يسهل الوصول إليها ومعالجتها وتحليلها بطرق فعالة ومنظمة. أي أن فهم هذه الهياكل واستخدامها بشكل صحيح يسهم بشكل كبير في تحسين أداء النظم والتطبيقات الحاسوبية عبر تسهيل عمليات البحث، الإدراج، والحذف بكفاءة عالية.

تنفيذ الشجرة Tree Implementation

رغم اختلاف أنواع هياكل البيانات الشجرية Tree Data Structure إلا أنها تتشارك العمليات الأساسية لبنية بيانات الشجرية، ومن أهم هذه العمليات:

• الإنشاء (Create) : إنشاء الشجرة.
• الإدراج (Insertion): إضافة عقدة جديدة إلى الشجرة.
• الحذف (Deletion): إزالة عقدة من الشجرة.
• البحث (Search): إيجاد عقدة معينة في الشجرة.
• التنقل (Traversal): زيارة العقد المختلفة في الشجرة بترتيب معين. الأنواع الشائعة للتنقل تشمل:
• Pre-order Traversal: زيارة العقدة الحالية ثم الأبناء من اليسار إلى اليمين.
• In-order Traversal: زيارة العقدة اليسرى، ثم العقدة الحالية، ثم العقدة اليمنى.
• Post-order Traversal: زيارة الأبناء من اليسار إلى اليمين، ثم العقدة الحالية.

ويمكن تنفيذ العمليات الأساسية لأي نوع من أنواع هياكل البيانات الشجرية بأشكال متعددة و باستخدام لغات برمجة متنوعة. في المثال التالي سنقوم بإنشاء شجرة بيانات من نوع N-ary Tree بإستخدام لغة  C#  . سنبدأ بتعريف العقدة والشجرة، ثم نضيف عمليات الإدراج، البحث، الحذف، والتنقل.

نبدأ أولا بتعريف العقدة : لتعريف هيكل العقدة Node لهذا سننشئ Node class بحيث يحتوي على مفتاح وقائمة من الأبناء في المثال استخدمنا قائمة من نوع List.

public class Node
{
    public int Key;
    public List<Node>Children;

    public Node(int key)
    {
        Key = key;
        Children = new List<Node>();
    }
}

العمليات على الشجرة ننشئ NaryTree class حيث يشمل العمليات الأساسية مثل الإنشاء، الإدراج، البحث، الحذف، والتنقل. كتالي:

الإنشاء (Create) : إنشاء الشجرة في هذه الخطوه نقوم بتعريف هيكل الشجرة NaryTree بحيث يحتوي على الجذر.

public class NaryTree
{
    public Node Root;

    public NaryTree()
    {
        Root = null;
    }
...........

الإدراج (Insertion): يتم إدراج عقدة جديدة كطفل لعقدة الأب إذا كان الأب غير موجود، يتم تعيين الجذر للعنصر الجديد إذا كان الجذر فارغًا.

...........
  //The method for inserting a node
    public void Insert(Node parent, int key)
    {
        if (parent != null)
        {
            parent.Children.Add(new Node(key));
        }
        else
        {
            if (Root == null)
            {
                Root = new Node(key);
            }
            else
            {
                Console.WriteLine("Parent is null and tree already has a root.");
            }
        }
    }
...........

البحث (Searching): يتم البحث عن عقدة معينة عبر التنقل في الشجرة.

...........
//The searching method
    public Node Search(Node node, int key)
    {
        if (node == null)
            return null;

        if (node.Key == key)
            return node;

        foreach (var child in node.Children)
        {
            var result = Search(child, key);
            if (result != null)
                return result;
        }
        return null;
    }
...........

الحذف (Deletion): يتم حذف عقدة معينة من قائمة الأطفال لعقدة الأب.

...........
//The method for deleting a node
    public void Delete(Node parent, int key)
    {
        if (parent == null)
            return;

        for (int i = 0; i < parent.Children.Count; i++)
        {
            if (parent.Children[i].Key == key)
            {
                parent.Children.RemoveAt(i);
                return;
            }
            else
            {
                Delete(parent.Children[i], key);
            }
        }
    }
...........

التنقل (Traversal): يتم استعراض العقد باستخدام التنقل (Traversal) وتتعدد أنواع التنقل في المثال سنستخدم ترتيب ما قبل (Pre-order Traversal) حيث يتم زيارة العقدة الحالية ثم الأبناء من اليسار إلى اليمين.

...........
//The Preorder Traversal method
    public void PreorderTraversal(Node node)
    {
        if (node == null)
            return;

        Console.Write((char)node.Key + " ");
        foreach (var child in node.Children)
        {
            PreorderTraversal(child);
        }
    }
}

طريقة الاستدعاء و الاستخدام في الدالة Main

...........
 public static void Main()
    {
        NaryTree tree = new NaryTree();
        tree.Root = new Node('A');  //Creating the root node

        // Inserting children nodes to the root
        tree.Insert(tree.Root, 'B');
        tree.Insert(tree.Root, 'C');
        tree.Insert(tree.Root, 'D');
        
        //Inserting children nodes for the B node  
        Node node2 = tree.Search(tree.Root, 'B');
        if (node2 != null)
        {
            tree.Insert(node2, 'E');
            tree.Insert(node2, 'F');
        }
        
        // Inserting children nodes for the C node 
        Node node3 = tree.Search(tree.Root, 'C');
        if (node3 != null)
        {
            tree.Insert(node3, 'G');
            tree.Insert(node3, 'H');
            tree.Insert(node3, 'I');
        }
        //Inserting a node child for D node 
        Node node4 = tree.Search(tree.Root, 'D');
        if (node4 != null)
        {
            tree.Insert(node4, 'J');
        }
        
         //inserting a child to J node
        Node node5 = tree.Search(node4, 'J');
        if (node5 != null)
        {
            tree.Insert(node5, 'K');
        }
        Console.WriteLine("Pre-order traversal of the tree:");
        tree.PreorderTraversal(tree.Root);
        Console.WriteLine();

        Console.WriteLine("Delete node with key 'K':");
        tree.Delete(tree.Root, 'K');
        tree.PreorderTraversal(tree.Root);
        Console.WriteLine();
    }
...........

الكود للمثال بالكامل على الرابط هنـا كما يمكن مقارنة طريقة تطبيق المثال مع تنفيذه بلغة C على الرابط هنـا، أيضاً يمكننا توسيع الكود لإضافة المزيد من العمليات أو لتحسين الأداء وفقًا لاحتياجاتنا.

تُعد هياكل البيانات الشجرية (Trees Data Structures) أساسية في العديد من التطبيقات البرمجية، وتُستخدم بفعالية لتنظيم ومعالجة البيانات بطريقة سريعة وفعالة.لهذا فإن الإلمام بهياكل البيانات الشجرية يعزز من قدرات المبرمجين على تصميم حلول فعالة ومرنة لمشاكل البيانات المعقدة. إن تبني وفهم هذه الهياكل يمكن أن يؤدي إلى تحسينات كبيرة في أداء التطبيقات، ويساهم في تطوير برمجيات أكثر قوة واستجابة للمتطلبات.