كفاءة الخوارزميات والـ Big-O

كفاءة الخوارزميات والـ Big-O

ماهي الحالات العامة لقياس أداء الخوارزميات..؟! وما علاقتها برموز قياس كفاءة الخوارزميات..؟؟!! ماهو مقياس كفاءة الخوارزمية Big-O ..؟! وكيف يتم تحليل الخوارزميات واحتساب كفاءتها بالمقياس Big-O..؟! تعرف ايضاً على أشهر الخوارزميات والـ Big-O لها

في مقالات سابقة مثل مقدمة في الخوارزميات و أداء الخوارزميات تحدثنا عن عن كفاءة الخوارزمية، حيث أوضحنا أن كفاءة الخوارزمية Algorithm Efficacy تُميز بتعقيد المساحة Space Complexity وتعقيد الوقت Time Complexity . كما أوضحنا كيف يرتكز إطار تحليل الكفاءة على ترتيب نمو عدد العمليات الأساسية للخوارزمية كمؤشر رئيسي لكفاءة الخوارزمية. واهـم الدوال للمقارنة ترتيب النمو.في هذا المقال سنتحدث عن مقاييس كفاءة الخوارزميات ولماذا نعتمد Big-O دائماً، لنبدأ...

في هذا المقال سنتعرف على :

• حالات قياس أداءالخوارزميات.
• رموز قياس كفاءة الخوارزميات.
• عن مقياس تعقيد الخوارزميات Big-O.
• تحليل كفاءة الخوارزميات بالمقياس Big-O.
• دوال ترتيب النمو والـ Bio-O لها.
• أشهر الخوارزميات والـ Big-O لها .

حالات قياس أداء الخوارزميات

عندما نتحدث عن أداء الخوارزمية فإننا نعني كفاءة الخوارزمية أي مستوى تعقيد الخوارزمية و مصطلح تعقيد الخوارزمية Algorithm complexity هو ببساطة مقدار العمل الذي تؤديه الخوارزمية لإكمال مهمتها، ويستخدم علماء الكمبيوتر ثلاثة حالات لتمثيل هذا التعقيد وهي:

الحالة الأسوأ Worse case (usually)

وتتمثل في الدالة التي تصف سلوك الخوارزمية عند استهلاك الحد الأقصى من الوقت المتوقع لتنفيذ خوارزمية بحجم n من المدخلات ( أي أن تقوم الخوارزمية باختبار جميع المدخلات ) وهي الحالة التي عادة ما تحدث فهي تعطي حدًا أعلى مضمونًا لوقت التشغيل لأي إدخال. أي أن:

g(n) = maximum time of an algorithm on any input of size n.

الحالة الاعتيادية Average case (sometimes)

وتتمثل في الدالة التي تمثل الوقت النموذجي لإعطاء نتيجة الخوارزمية ففي هذه الحالة تنفذ الخوارزمية على عدد مناسب من المدخلات وهذه الحالة تحدث في بعض الاحيان وتحتاج إلى افتراض التوزيع الإحصائي للمدخلات.وهذا يعني:

g(n) = expected time of an algorithm over all input of size n.

الحالة الأفضل Best case (NEVER)

وتتمثل في الدالة التي تصف سلوك الخوارزمية عند استهلاك الحد الأدنى من الوقت المتوقع لتنفيذ خوارزمية بحجم n من المدخلات ( مثال عليها خوارزمية بحث تجد النتيجة المطلوبة في اول مدخل ) وهذه الحالة قد لاتحدث مطلقاً للاحتمال نتائج خاطئة باستخدام خوارزمية بطيئة تعمل بسرعة على بعض المدخلات.

تطبيق حالات قياس أداء الخوارزميات

مثال : لكي يتضح مفهوم حالات قياس أداء الخوارزميات بشكل أفضل دعونا نطبقها على خوارزمية Sequential Search

Algorithm : 
Sequential Search (A[0…..n-1], k) 
//searches for a given value in a given array by sequential search 
//Input: An array A[0….n-1] and a search key K
//Output: The index of the first element of A that matches K or -1 if there are no matching elements 
i = 0
while i < n and A[i] != K do
i = i + 1
if i < n return i
else return -1

• وهنا في الحالة الأسوأ worse case سيكون لدينا عدد n من من عمليات المقارنة.
• أما في أفضل الحالات best case سيكون عدد المقارنات لدينا يساوي 1.
• وفي المتوسط average case فيحسب عدد المقارنات كالتالي : 2/(n+1) على افتراض أن k موجود في المصفوفة A إذن يمكن القول:

Average case = (worse case + best case ) / 2

بالطبع لا يتم قياس اداء الخوارزميات بهذه الطريقة، هنالك رموز يستخدمها علماء الكمبيوتر للتحليل تعقيد الخوارزمية في تحليل الأداء هذه الرموز هي رموز مقاربة فئات الكفاءة الأساسية Asymptotic Notations Basic Efficiency Classes وأشهر هذه الرموز هو Big-O.

رموز قياس أداء الخوارزميات

هنالك رموز يستخدمها علماء الكمبيوتر للتحليل تعقيد الخوارزمية وتسمى موز مقاربة فئات الكفاءة الأساسية Asymptotic Notations Basic Efficiency Classes، واشهر هذه الرموز ثلاثة وهي رموز شائعة الاستخدام في تحليل الأداء وهي طريقة لمقارنة الدوال بحيث تتجاهل العوامل الثابتة و حجم المدخلات الصغير (أي عندما تمثل الخوارزمية في كثيرة حدود فإن ننعى بدراسة الحد الاعلى دون عامله ونتجاهل بقية الحدود ) وهذه الرموز هي :

Big-Oh notation (Worse Case)

Big-O وينطق "بق او" وتمثل الـ Big-O الحالة الأسواء هنا يتم اختبار الخوارزمية على جميع المدخلات هنا يكون معدل نمو للدلة الحالة الطبيعية  t(n) أبطأ من دالة الـ Big-O   g(n) ،ويعبر عن مقياس الـ Big-O بالرمز   O( g(n))   كما يتضح معنا في الشكل التالي:

Big-Theta notation (Average Case)

Bib-Theta وتنطق "بق ثيتا " ويعبر عن هذه المقياس بالرمز   Θ( g(n))   وهو تمثيل للحالة الاعتيادية لقياس أداء الخوارزمية أي بمعدل النمو مقارب او المساوي للحالة الطبيعية   t(n) ، وعند تمثيل الحالة الاعتيادية بمعادلة  g(n) ، ستكون حالات مقياس Big-Theta كم يتضح معنا في الشكل التالي:

Big-Omega notation (Best Case )

Big-omega وتنطق "بق أوميجا" ويرمز لهذه المقياس بالرمز  Ω(g(n))  وهو يمثل الحالة الأفضل Best case من حالات قياس الأداء للخوارزميات، وهنا سيكون معدل نمو دالة الـ Big-Omeg الـ  g(n) على الاقل أسرع من معدل النمو للدالة في الحالة الطبيعية  t(n) ، كما يتضح معنا في الشكل التالي:

تطبيق قياس أداء الخوارزمية باستخدام رموز قياس أداء الخوارزميات

في هذا المثال سنقوم بوصف حجم المدخلات inputs ثم نقوم بحساب عدد الخطوات steps لمعالجة هذا العدد من المدخلات حيث ان الخطوة الواحدة تمثل بـعملية اولية مثل  +, < , = , A[i] ، ثم سنقوم بعمل خوارزمية لداله تقوم بجمع عناصر مصفوفة معطاة وترجع نتيجة الجمع.

المدخلات Inputs هنا عبارة عن مصفوفة بطول n إذن حجم المدخلات = n. ويوضح الشكل التالي طريق احتساب خطوات التنفيذ للخوارزمية.

نلاحظ هنا:

• الخطوات 1, 2, 8 تنفذ للمرة واحدة
• الخطوات 3, 4, 5, 6, 7 يتكرر تنفيذها n من المرات.
• عليه فالدالة التي تمثل الخوازمية ستكون مجموع عدد خطوات التنفيذ f(n) = 5n + 3 هذه الدالة تسمى دالة التعقيد للخوارزمية complexity function of the algorithm

وعندما نريد تمثل ترتيب النمو بالرموز   Big-O و   Big-Θ و   Big- Ω للدالة  f(n) فستكون كالتالي:

O( f(n)) = O(n)

Ω( f(n)) = 1

Θ( f(n)) = (n +1) /2

وعادة ما يعتمد مقياس الـ Big-Oh لحساب تعقيد الخوارزمية هذا لأنه يمثل الحالة التي تغطي الحد الأقصى من المدخلات فيمكن القول أن التعقيد في هذا المثال يتمثل بـ   O(n)  .

عن مقياس تعقيد الخوارزميات Big-O

تدوين Big-O notation هو تدوين رياضي يستخدم لوصف السلوك المحدود لوظيفة ما عندما تقترب المعادلة من قيمة معينة أو ما لا نهاية. في علوم الكمبيوتر ، يتم استخدامه بشكل شائع لتحليل تعقيد الوقت ومساحة الذاكرة للخوارزميات.

وتعد Big-O واحدة من المفاهيم الأساسية في علوم الكمبيوتر والرياضيات التي تستخدم لتحليل كفاءة الخوارزميات وحساب التكلفة الزمنية لعمليات البرمجة. وهي عبارة عن رمز يستخدم لتحديد معدل نمو الوقت أو الذاكرة المطلوبة لتشغيل الخوارزمية والتي تعتبر من أهم المعايير التي يجب أن تأخذ بعين الاعتبار عند تصميم البرمجيات.

تساعد Big-O على تحديد العلاقة بين حجم المدخلات والوقت اللازم لإجراء معالجة البيانات، وتستخدم لتصنيف الخوارزميات حسب كفاءتها وأدائها. فعلى سبيل المثال، يمكن أن تكون الخوارزمية بتعقيد O(1)، وهذا يعني أنها تتطلب وقتاً ثابتاً لإجراء المعالجة بغض النظر عن حجم البيانات، بينما يمكن للخوارزمية بتعقيد O(n) أن تتطلب وقتاً يتناسب بشكل مباشر مع عدد المدخلات.

يوفر تدوين Big-O notation طريقة لمقارنة كفاءة الخوارزميات المختلفة من خلال التعبير عن السيناريو الأسوأ لمقدار الوقت أو المساحة المطلوبة لحل مشكلة كدالة لحجم الإدخال. و تسمح Big-O للمطورين باتخاذ قرارات مستنيرة بشأن الخوارزمية التي يجب استخدامها في مشكلة معينة بناءً على قابلية التوسع وخصائص الأداء.

يتم تحديد Big-O من خلال دراسة الحد الأقصى لعدد العمليات اللازمة لإجراء المعالجة في الخوارزمية، بما يعرف باسم تحليل الحالة الأسوأ. وتستخدم هذه المفاهيم والتقنيات في الكثير من مجالات الحوسبة، مثل تصميم الخوارزميات وتحليل البيانات، وتعتبر أداة أساسية للمطورين الذين يرغبون في تحسين أداء البرمجيات وتقليل التكلفة الزمنية والمالية.

تحليل كفاءة الخوارزميات بالمقياس Big-O

هنـا بعض الأمثلة عن طريقة احتساب Big-O بطريقة بسيطة

المثال الأول :

int sum = 1,i;
for ( i = 0; j < 100; i++)
	sum = sum + i

هنـا نتوقع تنفيذ جملة for عدد 100 مرة

وهناك 4 من الخطوات تنفذ لمرة واحدة إذن سيكون Big-O لها  O(1)

إذن الـ Big-O سيكون   O(100* 1) = O(1) * 100 = O(1) =  

المثال الثاني :

bool done = false;
int  result = 1 ,n;
scanf( "%d" , &n);
while (!done) {
	result = result *n;
	n--;
	if ( n<= 1) done  = true;
}

هنا نتوقع ان تكون قمية done = true عندما تنفذ جملة while عدد n من المرات فسيكون الـ O(n)= Big-O

المثال الثالث :

int j,k;
for ( j= 0; j < n; j++)
	for( k = n; k > 0; k--)
		sum += k + j;

هنـا نتوقع ان تكرر كلاً من جُمل for عدد n من المرات فسيكون Big-O = O(n²) = O (n *n)

دوال ترتيب النمو والـ Bio-O لها

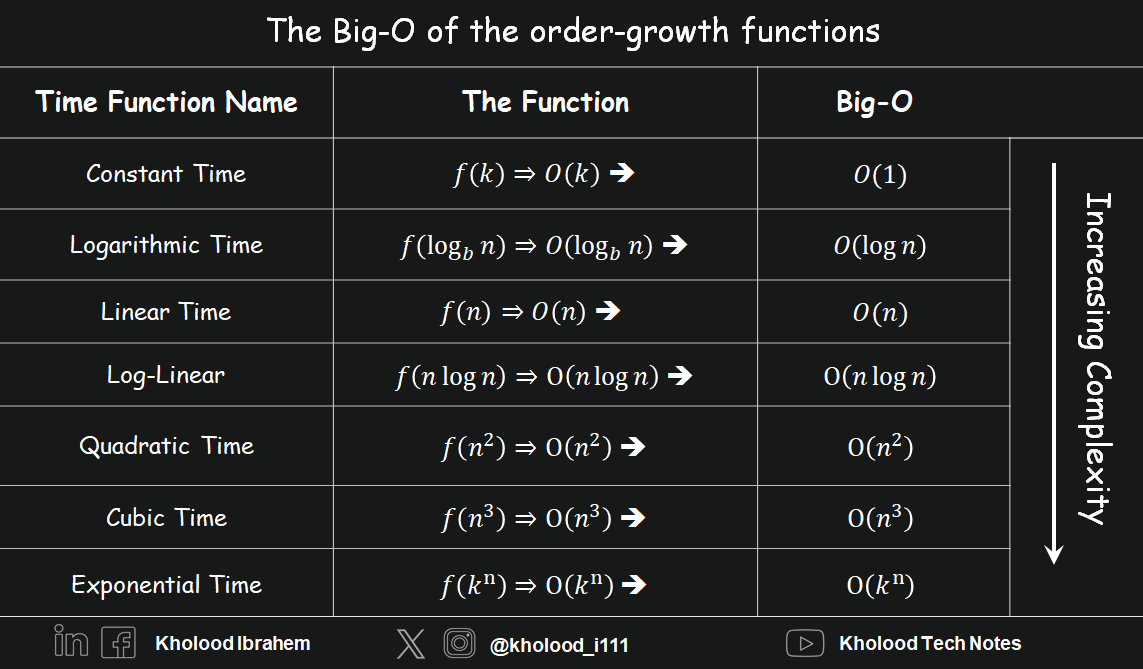
من الأمثلة في الفقرة السابقة وعلى افتراض أن n يمثل حجم المدخلات و b & k ثوابت يمكن أن نستنتج أنه سيكون تعقيد الـ Big-O للدوال ترتيب النمو كما يتضح معنا في الشكل التالي:

المزيد عن دوال ترتيب النمو في مقال عن أداء الخوارزميات .

أشهر الخوارزميات والـ Big-O لها

هناك العديد من الخوارزميات التي يمكن تصنيفها وفقًا لتعقيدها الزمني، ومن بين أشهر هذه الخوارزميات والـ Big-O لها:

• خوارزمية البحث الثنائي (Binary Search): تعقيد  O( log n) ، حيث تستغرق الخوارزمية وقتًا أقل مع زيادة حجم البيانات.
• خوارزمية الفرز السريع (Quick Sort): تعقيد   O( n log n ) في أفضل الحالات و  O(n²) في أسوأ الحالات.
• خوارزمية الفرز المدمج (Merge Sort): تعقيد   O(n log n ) ، وتستخدم لفرز مجموعة كبيرة من البيانات.
• خوارزمية فرز الفقاعة (Bubble Sort) : تعقيد   O(n²) في أسوأ الحالات،)، حيث يزداد وقت التنفيذ بشكل متناسب مع زيادة حجم المصفوف
• خوارزمية الفرز بالإختيار (Selection Sort) : تعقيد  O(n²) يزداد وقت التنفيذ بشكل متناسب مع زيادة حجم المصفوفة. وبالرغم من أن الفرز بالاختيار يعد واحدًا من أبسط الخوارزميات لفرز البيانات، إلا أنه يستخدم بشكل محدود في التطبيقات الحقيقية بسبب كفاءته المنخفضة في حالة المصفوفات الكبيرة
• خوارزمية البحث الخطي (Linear Search): تعقيد  O ( n ) ، حيث تستغرق الخوارزمية وقتًا يتناسب مباشرة مع عدد العناصر في البيانات.
• خوارزمية قاعدة السلم (Staircase Search): تعقيد  O(n) في أسوأ الحالات، وتستخدم للبحث عن عنصر في مصفوفة مرتبة بشكل تصاعدي.
• خوارزمية البحث في العمق أولاً (Depth-First Search): تعقيد   O ( V + E ) ، حيث V هو عدد العقد و E هو عدد الحواف في الرسم البياني.
• خوارزمية البحث في العرض أولاً (Breadth-First Search): تعقيد  O ( V + E ) ، وتستخدم للبحث عن الأساليب الأكثر شيوعًا في ترتيب الجداول والمخططات.
• خوارزمية زراعة الأشجار (Tree Traversal): تعقيد  O ( n ) ، وتستخدم لترتيب البيانات في شكل شجري.
• خوارزمية البحث في الهاش (Hash Search): تعقيد  O ( 1 ) في أفضل الحالات، و  O ( n ) في أسوأ الحالات، وتستخدم لتخزين والبحث عن البيانات في جداول الهاش.
• خوارزمية البحث العشوائي (Randomized Search): تعقيد  O ( n ) في المتوسط، وتستخدم للبحث عن عنصر عشوائي في مجموعة من البيانات.

ويوضح الشكل التالي الـ Big-O لأشهر الخوارزميات بشكل مبسط

إلى هنا ينتهي هذا المقال الذي تعرفنا فيه الحالات العامة لقياس الخوارزميات ومايمثلها من رموز مقاربة فئات الكفاءة الأساسية، وأمثلة على طريقة تحليل الخوارزمية واحتساب مقاييس الأداء لها، عرفنا لماذ يتم اعتماد مقياس الـ Big-O دائما كمقياس رئيسي لقياس كفاءة الخوارزمية، مع أمثلة على طريقة تحليل الخوارزميات وحساب الـ Big-O لها..